Bit-Pair-Verfahren

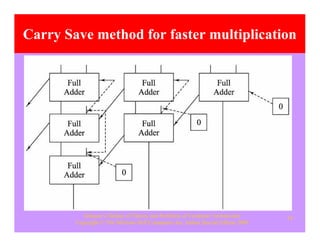
Das Bit-Pair-Verfahren (eng. Bit-Pair-Recoding) ist ein Algorithmus zur Beschleunigung computergestützter Multiplikation zweier Zahlen in Zweierkomplement-Darstellung. Er stellt eine Erweiterung des Booth-Algorithmus dar.

Idee

Wird eine Zahl ${\displaystyle x}$ mit 2 multipliziert und anschließend von der entstandenen Zahl subtrahiert, ergibt sich wieder ${\displaystyle x}$:

• ${\displaystyle 2x-x=x}$

Analog:

• ${\displaystyle -2x x=-x}$

Der Booth-Algorithmus allerdings generiert unter Umständen Code, der solche (unnötigen) Berechnungen durchführen würde. Das lässt sich durch das Bit-Pair-Verfahren vereinfachen.

Verfahren

Benachbarte „*( 1)“ und „*(-1)“ im Booth-Code werden wie folgt zusammengefasst:

Es entfällt eine Addition. Die Berechnung wird effizienter.

Beispiel

Es soll ${\displaystyle 3*89}$ berechnet werden.

• ${\displaystyle 3_{10}=00000011_{2}}$
• ${\displaystyle 89_{10}=01011001_{2}}$

Auf den Faktor 89₁₀ werden nacheinander die entsprechenden Verfahren angewandt:

Die Berechnung erfolgt analog zum Booth-Algorithmus:

• ${\displaystyle 0100001011_{2}=267_{10}=3_{10}*89_{10}}$

Das Ergebnis ist korrekt, ausgeführt allerdings mit 4 Additionsoperationen, statt mit 6. Es sei angemerkt, dass hier nur zu Beispielzwecken 89 statt 3 mit den Algorithmen vereinfacht wurde. Praktisch wäre es natürlich in diesem Fall am effizientesten 89 * 3 „direkt“ zu berechnen. Das würde nur 2 Additionen erfordern.

Literatur

• Arithmetic Multiplication Circuits (engl.; PDF-Datei; 134 kB)
• T. N. Rajashekhara, O. Kal: Fast multiplier design using redundant signed-digit numbers. In: International Journal of Electronics. Band 69, Nr. 3, September 1990, ISSN 0368-1947, S. 359–368, doi:10.1080/00207219008920321.